专题21.1二次根式数学华东师大版九年级上册

【题型1 二次根式的概念】
1.定义：一般地，我们把形如a(α≥0)的式子叫做二次根式，“√”叫做二次根号，α叫做被开方数。
2.拓展：二次根式必须同时满足两个条件：（1）含二次根号“√”；（2）被开方数必须是非负数（被开方数可以是数字也可以是含有字母的式子）。
【知识点2 二次根式有无意义的条件】
当a≥0时，二次根式√a有意义；当a<0时，二次根式√a无意义。例如：因为x²+2x+1=(x+1)²≥0，所以二次根式√(x²+2x+1)恒有意义。
【知识点3 二次根式的性质】
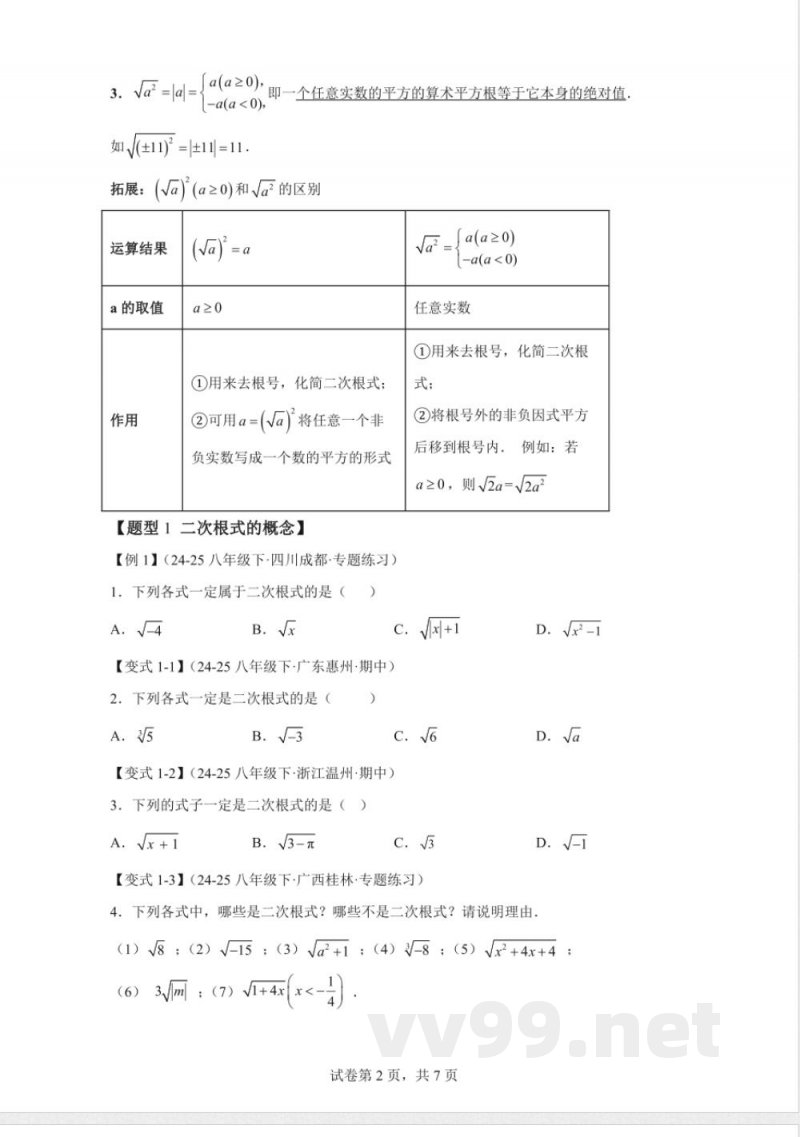
1. 二次根式√a具有双重非负性：被开方数a≥0，二次根式√a≥0。
2. (√a)²=α(α≥0)，即两个非负数的算术平方根的平方等于它本身，如(√5)²=5。
3. √a=|a| (a≥0)，即任意实数a的平方的算术平方根等于它本身的绝对值，如(√11)²=±11=11。
【例1】（24-25 八年级下·四川成都·专题练习）
1. 下列各式一定属于二次根式的是：（A. √-4，B. √x，C. a (a≥0)，D. a (a<0)）。
2. 下列各式一定是二次根式的是：（A. 5，B. -3，C. √6）。
3. 下列的式子一定是二次根式的是：（A. √x+1，B. √3-元，C. 3）。

说明:本文档为学习资料，仅供教学与自学使用，资源免费下载，不含任何诱导下载或捆绑程序。