浙教版九年级数学上册单元测试题

第1章 浙教版九年级数学上册单元测试题
一、选择题（每题3分，共30分）
1．下列函数中是二次函数的是（）
A. y = 3x - 1
B. y = 3x² - 1
C. y = (x + 1)² - x²
D. y = x² - 1
2. 对于二次函数y = 3(x - 2)² + 1的图象，下列说法正确的是（）
A. 开口向下
B. 对称轴是直线x = -2
C. 顶点坐标是(2, 1)
D. 与x轴有两个交点
3. 抛物线y = x² - 1可由下列哪一个函数的图象向右平移1个单位，再向下平移2个单位得到？（）
A. y = (x - 1)² + 1
B. y = (x + 1)² + 1
C. y = (x - 1)² - 3
D. y = (x + 1)² + 3
4. 二次函数y = x² - 2x + 1的图象与x轴的交点个数是（）
A. 0
B. 1
C. 2
D. 3
5. 若y1, y2, y3为二次函数y = x² + 4x - 5的图象上的三点，则y1, y2, y3的大小关系是（）
A. y1 > y2 > y3
B. y2 > y1 > y3
C. y3 > y1 > y2
D. y1 > y3 > y2
6. 在同一坐标系中，二次函数y = ax² + bx与一次函数y = bx - a的图象可能是（）
A. 相交于两点
B. 相交于一点
C. 没有交点
D. 相交于三点
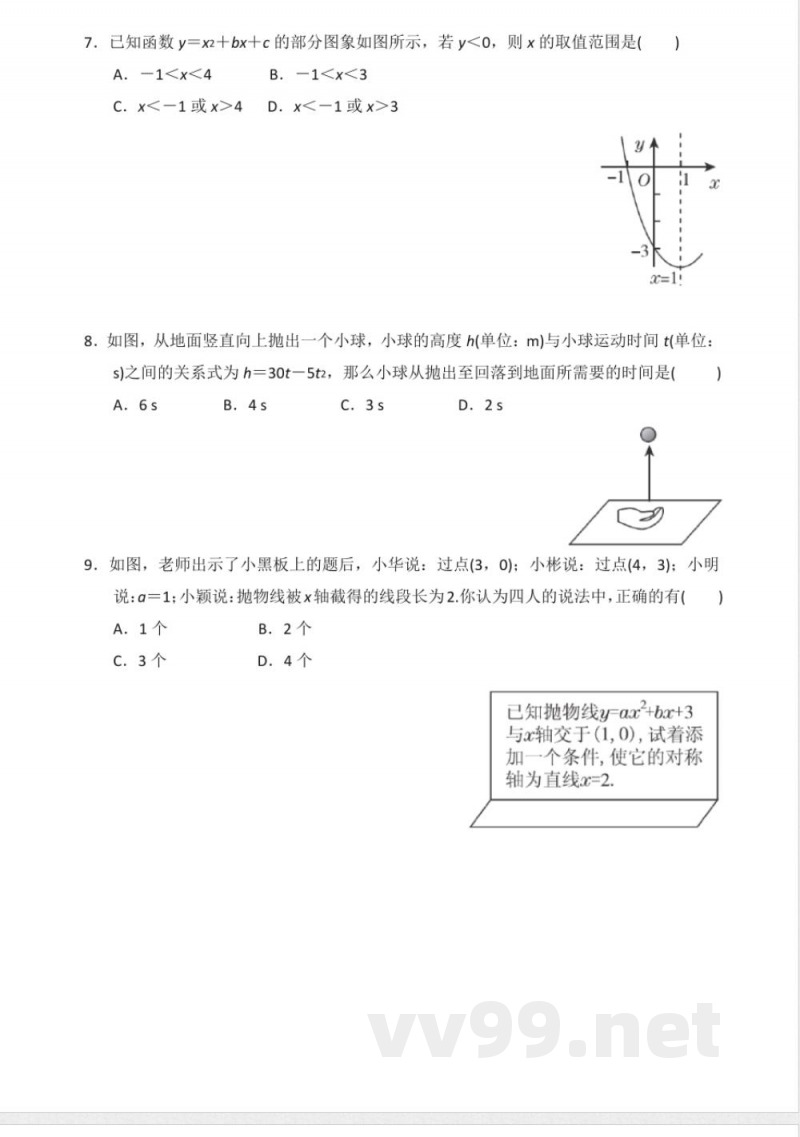
7. 已知函数y = x² + bx + c的部分图象如图所示，若y < 0，则x的取值范围是（）
A. -1 < x < 4
B. -1 < x < 3
C. x < -1 或 x > 4
D. x < -1 或 x > 3
8. 如图，从地面竖直向上抛出一个小球，小球的高度h(单位：m)与小球运动时间t(单位：s)之间的关系式为h = 30t - 5t²，那么小球从抛出至回落到地面所需要的时间是（）
A. 6s
B. 4s
C. 3s
D. 2s
9. 如图，老师出示了小黑板上的题后，小华说：过点(3, 0)；小彬说：过点(4, 3)；小明说：α = 1；小颖说：抛物线被x轴截得的线段长为2。你认为四人的说法中，正确的有（）
A. 1个
B. 2个
C. 3个
D. 4个
10. 已知抛物线y = x² + bx + c与x轴的一个交点的坐标为(1, 0)，试着添加一个条件，使它的对称轴为直线x = 2。

二、填空题（每题3分，共24分）
11. 抛物线y = -x² + 15的顶点坐标是（）
12. 函数y = x² + 2x + 1，当y = 0时，x =（）
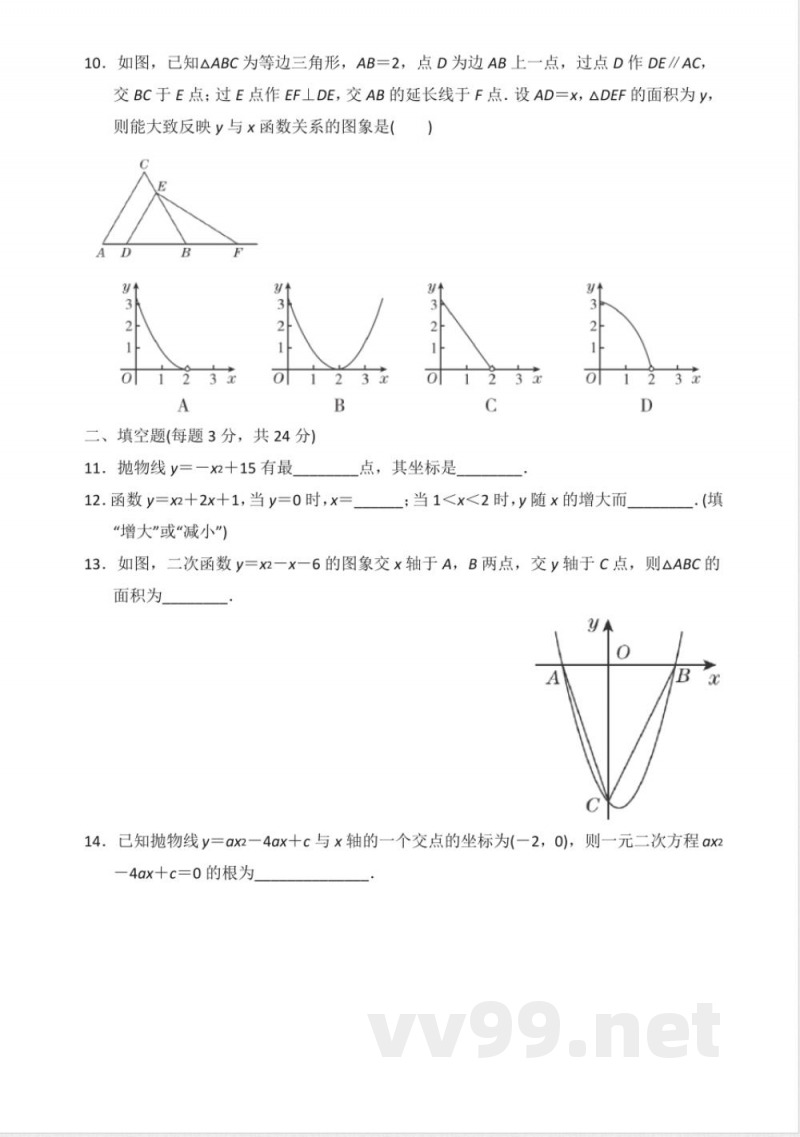
13. 如图，二次函数y = x² - x - 6的图象交x轴于A，B两点，交y轴于C点，则AABC的面积为（）
14. 已知抛物线y = ax² - 4ax + c与x轴的一个交点的坐标为(-2, 0)，则一元二次方程ax² - 4ax + c = 0的根为（）
15. 已知二次函数y = ax² + bx + c与一次函数y = kx + m的图象相交于点A(-2, 4)，B(8, 2)，则能使y > y成立的x的取值范围是（）
16. 某涵洞的截面是抛物线形，如图所示，在图中建立的直角坐标系中，抛物线的表达式为y = 14x²，当涵洞水面宽AB为12m时，水面到桥拱顶点O的距离为（）
17. 对于二次函数y = x² - 2mx - 3，有下列说法：①它的图象与x轴有两个交点；②如果当x = 1时，y随x的增大而减小，则m = 1；③若图象向左平移3个单位后过原点，则m = -1；④如果当x = 4与x = 100时，函数值相等，则当x = 104时，函数值为-3，其中正确说法的序号是（）
18. 如图，把抛物线y = x²平移得到抛物线m，抛物线m经过点A(-6, 0)和原点O(0, 0)。

说明:本文档为学习资料，仅供教学与自学使用，资源免费下载，不含任何诱导下载或捆绑程序。