2.3《 用频率估计概率》同步练习 2025~2026学年（浙教版）数学九年级上册

1. 数学家皮尔逊为了研究概率问题，进行了大量重复抛硬币试验，并用频率来估计概率。当他把一枚硬币抛掷24000次时，正面朝上的次数与该实验结果比较符合的是（）A. 11011 B. 12012 C. 13013 D. 14014
2. 在一个不透明的箱子里装有m个球，其中红球4个，这些球除颜色外都相同，每次将球搅拌均匀后，任意摸出一个球记下颜色后再放回，大量重复试验后发现，摸到红球的频率在0.5，那么可以估算出m的值为（）。A. 8 B. 12 C. 15 D. 20
3. 在学习了“用频率估计概率”这一节内容后，某课外兴趣小组利用计算器进行模拟试验来探究“6个人中有2个人同月过生日的概率”。他们将试验中获得的数据记录如下：试验次数“有2个人同月过生日”的次数“有2个人同月过生日”的频率 100 800 0.83 200 290 0.76 350 392 0.78 400 1000 0.79 通过试验，该小组估计“6个人中有2个人同月过生日”的概率（精确到0.01）大约是（）。A. 0.80 B. 0.79 C. 0.78 D. 0.77
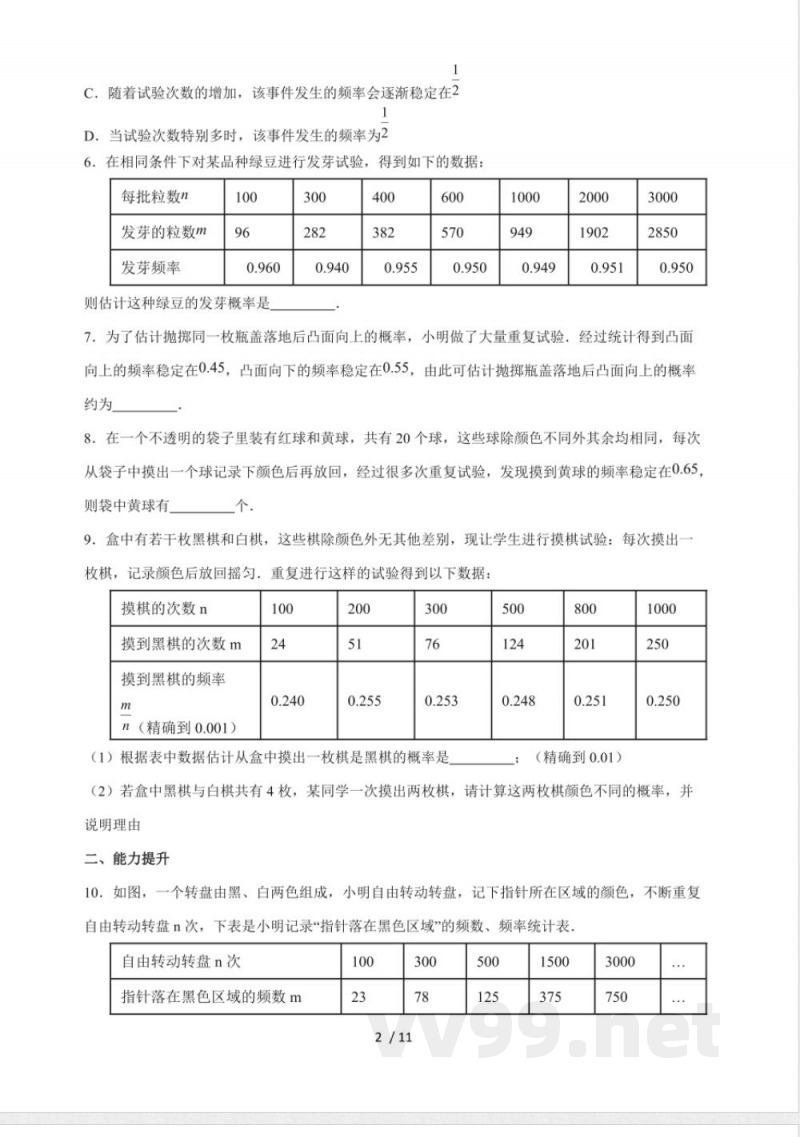
4. 某地区林业局考察一种树苗移植的成活率，将调查数据绘制成统计图，则可估计这种树苗移植成活的概率约是（）。A. 0.80 B. 0.85 C. 0.90
5. 若某随机事件发生的概率为2，则下列说法正确的是（）。A. 在2次试验中，该事件至少发生1次 B. 在1000次试验中，该事件发生的次数一定为500次 C. 随着试验次数的增加，该事件发生的频率会逐渐稳定在2 D. 当试验次数特别多时，该事件发生的频率为2
6. 在相同条件下对某品种绿豆进行发芽试验，得到如下的数据：每批粒数n 发芽的粒数m 发芽频率 100 96 0.96 300 282 0.94 400 380 0.95 600 570 0.95 1000 940 0.95。则估计这种绿豆的发芽概率是（）。
7. 为了估计抛掷同一枚瓶盖落地后凸面向上的概率，小明做了大量重复试验。经过统计得到凸面向上的频率稳定在0.45，凸面向下的频率稳定在0.55，由此可估计抛掷瓶盖落地后凸面向上的概率约为0.45。
8. 在一个不透明的袋子里装有红球和黄球，共有20个球，这些球除颜色不同外其余均相同，每次从袋子中摸出一个球记录下颜色后再放回，经过很多次重复试验，发现摸到黄球的频率稳定在0.65，则袋中黄球有（）。
9. 盒中有若干枚黑棋和白棋，这些棋除颜色外无其他差别，现让学生进行摸棋试验：每次摸出一枚棋，记录颜色后放回摇匀。重复进行这样的试验得到以下数据：摸棋的次数n 摸到黑棋的次数m 摸到黑棋的频率。n=100, m=24, 频率=0.24；n=200, m=51, 频率=0.255；n=300, m=76, 频率=0.253。根据表中数据估计从盒中摸出一枚棋是黑棋的概率是（）。A. 0.248 B. 0.250 C. 0.251
（2）若盒中黑棋与白棋共有4枚，某同学一次摸出两枚棋，请计算这两枚棋颜色不同的概率，并说明理由。

说明:本文档为学习资料，仅供教学与自学使用，资源免费下载，不含任何诱导下载或捆绑程序。